Which Expression Is Equivalent to mc001-1.jpg: Mastering Simplification and Algebraic Concepts
Unlocking the Secrets of Equivalent Expressions for Better Math Skills
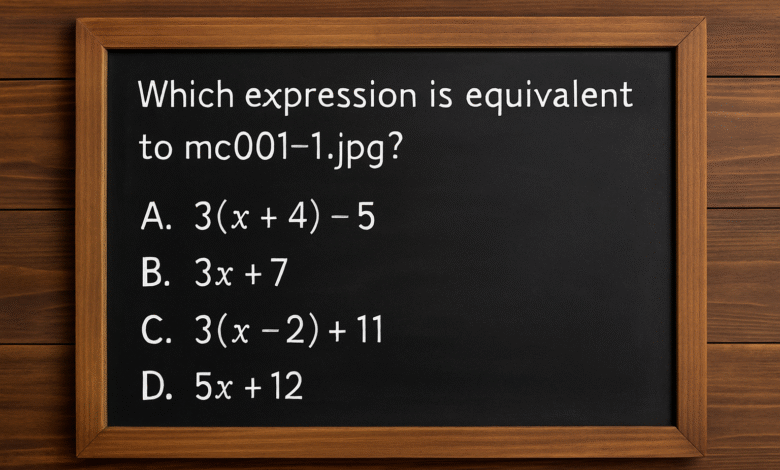
Introduction
Understanding which expression is equivalent to mc001-1.jpg is essential for solving many algebra problems accurately. In mathematics, especially in algebra, expressions often look different but may represent the same value. This concept is called equivalent expression, and it forms the foundation of simplifying, factoring, and solving equations. Many students face challenges when trying to determine whether two expressions are truly equivalent, but with the right strategies and knowledge, this process becomes much easier.
This article will explain how to simplify, expand, and factor expressions while combining like terms and using various properties such as the distributive property, commutative property, and associative property. By the end of this guide, you will not only know how to find the equivalent expression but also improve your problem-solving and critical thinking skills in algebra.
Understanding Equivalent Expressions
What Is an Equivalent Expression?
An equivalent expression is a mathematical phrase that may look different but has the same value as another expression. For example, 2(x+3)2(x + 3) and 2x+62x + 6 are equivalent because they simplify to the same result. Recognizing equivalent expressions is vital in algebra as it allows us to simplify complex problems and solve equations efficiently.
When identifying which expression is equivalent to mc001-1.jpg, you need to carefully apply rules of algebra, simplify exponents, and check for domain restrictions in rational expressions.
Why Equivalent Expressions Matter
Equivalent expressions are essential in many areas of math:
-
Solving equations – Simplifying both sides helps solve unknowns faster.
-
Graphing functions – Standard form, vertex form, and factored form represent the same quadratic but in different ways.
-
Real-world applications – Engineers, scientists, and economists rely on equivalent forms to model problems accurately.
Key Algebraic Operations for Simplifying Expressions
Combine Like Terms
The first step in simplification is to combine like terms. These are terms that have the same variable and exponent. For example, 3x+5x=8x3x + 5x = 8x. This process helps to rewrite expressions into a simplified form and is essential when solving algebraic identities.
The Distributive Property
The distributive property is one of the most powerful tools in algebra. It allows you to expand expressions by multiplying each term inside the parentheses by the factor outside:
a(b+c)=ab+aca(b + c) = ab + ac
This is particularly useful when working with polynomial identities and expanding complex equations.
The Commutative and Associative Properties
-
Commutative Property: Changing the order of numbers doesn’t change the result, such as a+b=b+aa + b = b + a.
-
Associative Property: Changing the grouping of numbers doesn’t change the result, such as (a+b)+c=a+(b+c)(a + b) + c = a + (b + c).
These properties are crucial for simplifying expressions and ensuring your steps are mathematically valid.
Factoring and Expanding Expressions
How to Factor
Factoring is the reverse of expanding. It involves breaking down an expression into simpler components, or factors. For example, x2+5x+6x^2 + 5x + 6 can be factored into (x+2)(x+3)(x + 2)(x + 3). Factoring is often used when working with rational expressions and solving quadratic equations.
Expanding Expressions
When you expand, you multiply the factors to rewrite them in standard form. For instance, (x+2)(x+3)=x2+5x+6(x + 2)(x + 3) = x^2 + 5x + 6. Understanding both factoring and expanding is crucial for identifying which expression is equivalent to another form.
Simplifying Complex Expressions
Rational Expressions and Domain Restrictions
A rational expression is a fraction where the numerator and denominator are polynomials. To simplify these, you factor both the numerator and denominator, then cancel common factors. However, you must consider domain restrictions, which are values that make the denominator equal to zero. Ignoring these can lead to errors even if the expressions seem equivalent.
Radical Expressions and Rationalizing the Denominator
When dealing with square roots, you often need to rationalize the denominator. For example:
12=22\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}
This step ensures the expression is in its most simplified form, which is especially important when comparing two expressions for equivalence.
Practical Steps to Identify Equivalent Expressions
Step 1: Simplify Both Expressions
Use combining like terms, factoring, and distributing to rewrite both expressions into their simplest forms.
Step 2: Compare Structures and Coefficients
For polynomials, check if both have the same variables and coefficients. This confirms they are equivalent.
Step 3: Substitute Test Values
Plug in different numbers to verify if both expressions yield the same result. This is a quick way to check your work.
Common Challenges and Solutions
Negative Signs and Parentheses
Students often misplace negative signs when distributing. Always double-check signs to avoid incorrect simplification.
Complex Fractions
When working with equivalent fractions, find a common denominator before simplifying. This makes combining fractions easier and helps identify equivalent rational expressions.
Conclusion
Understanding which expression is equivalent to mc001-1.jpg requires mastering algebraic techniques like simplifying, factoring, expanding, and combining like terms. By applying properties such as the distributive property, commutative property, and associative property, you can confidently identify equivalent expressions.
Remember to always check domain restrictions, rationalize denominators when needed, and verify your results by substitution. With consistent practice, you will develop the skills to solve algebra problems quickly and accurately.
FAQ
Q1: What is an equivalent expression in simple words?
An equivalent expression is a different-looking expression that has the same value as another.
Q2: Why is factoring important in finding equivalent expressions?
Factoring helps break down complex expressions into simpler parts, making it easier to compare and simplify.
Q3: How do you know if two rational expressions are equivalent?
Simplify both expressions completely and check domain restrictions to ensure they match exactly.
Q4: Can substitution alone prove equivalence?
Substitution is a quick check, but algebraic simplification is necessary for full proof.
Q5: Why is the distributive property essential?
It allows you to expand and simplify expressions systematically, which is key for finding equivalence.



